アイヤー!
現代ポートフォリオ理論の結論がなぜ”市場平均が最適ポートフォリオ”となるのか、その結論に至るまでの過程を解説します。
本当は一つの記事にまとめようと思ってたんですが、気づけば3回目になってましたw
前回の記事で接点ポートフォリオこそが最適ポートフォリオになることを説明しました。もしよければこちらも見てみてください。
現代ポートフォリオ理論の結論
ここからはかなり強引にも感じる理論なんですが、
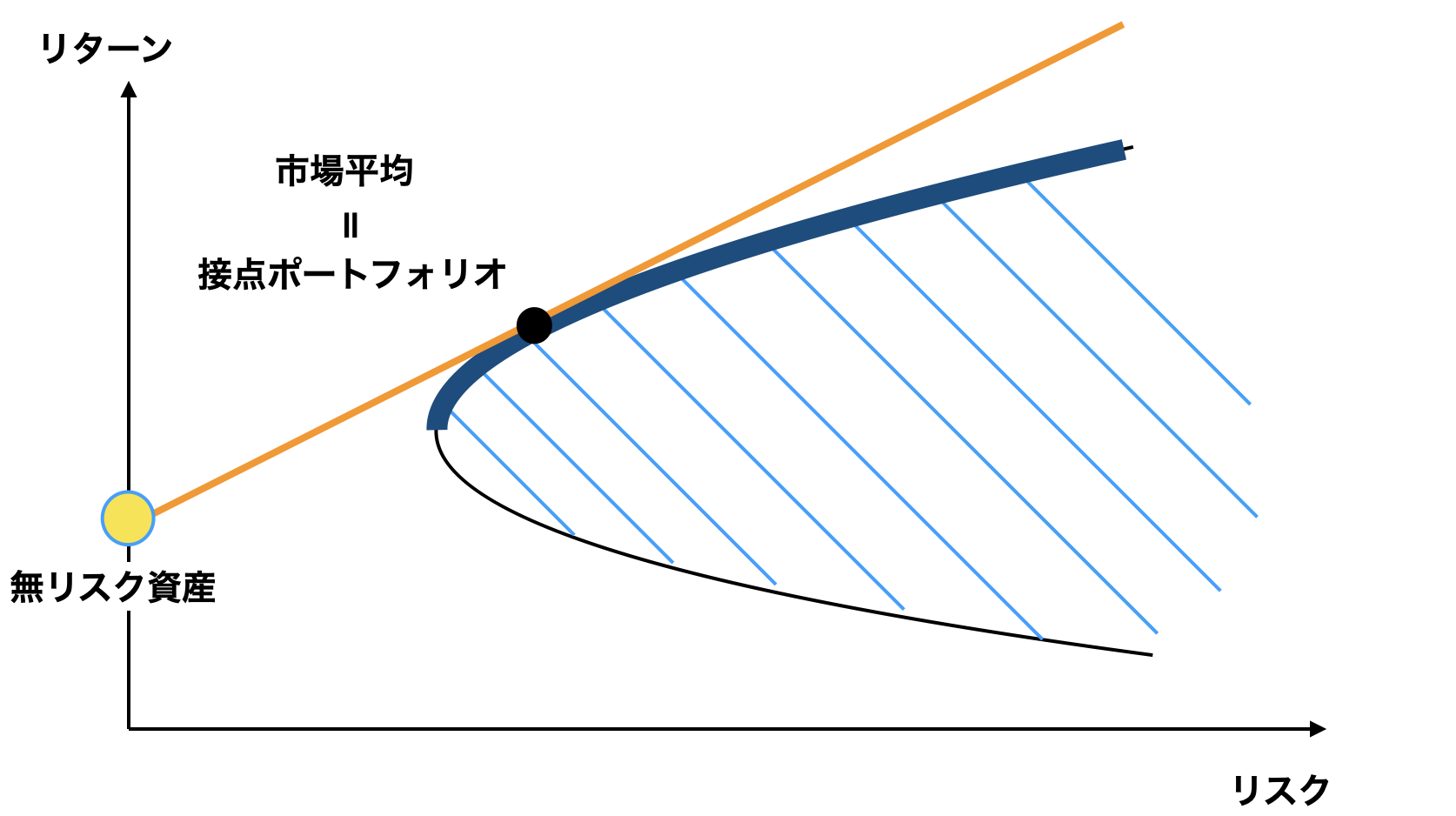
接点ポートフォリオが最適なポートフォリオならば、全ての投資家は接点ポートフォリオを保有するだろう。その結果、接点ポートフォリオが市場平均となる。
ということになります。これがいわゆる現代ポートフォリオ理論の結論で、市場平均こそが最適ポートフォリオとなる理由です。
どうでしょう?なかなかファンキーな考え方ですよねw
かなり大胆な仮定を置いていて、現実世界とはかけ離れた印象を持ってしまいます。
実際、ここでは3つの仮定を置いてます。
- 全ての投資家はリターンとリスクという2種類の情報のみを見て、投資判断を行う
- 全ての投資家はそれぞれの資産のリターンとリスクについて同じ値を想定している(リターン、リスクは用いるデータの期間を変えれば変わります)
- 全ての投資家は接点ポートフォリオに投資する
この仮定を置けば、市場平均が最適ポートフォリオという結論が導かれるわけですが、う〜ん、こんな状況あり得ないという感じがしてしまいます。
ただ、この疑問に対して、冨島 佑允さんの著書 ”投資と金融がわかりたい人のための ファイナンス理論入門” ではこのように言ってます。
「本当にこんな仮定を置いてしまっていいのか?」と心配に思われる方もいるでしょうが、現実世界の枝葉を取り除き、本質だけを残すことで明快な理論を構築するのが、学者の腕の見せ所なのです。
冨島 佑允. 投資と金融がわかりたい人のための ファイナンス理論入門 プライシング・ポートフォリオ・リスク管理
これって経済学とかでも同じだと思うんですけど、人間の行動って多種多様で不確実なものなので、複雑すぎてモデル化できないんですよ。そこでかなり大胆な仮定を置いて、いろんなものをバサッと切って、モデル化すると。
切り捨てるものが大きければ大きいほど、モデルの精度は下がりますが、それでも何も言えないよりは良いということですね。
注意すべき点
現実世界では、インデックス投資の優秀さは過去の実績から明らかにされています。ただ、接点ポートフォリオと市場平均は実際のところは乖離しているはずなので、現代ポートフォリオの話と結びつけていいのかはよくわかりませんw
現代ポートフォリオ理論の結論で勘違いしてはいけないところは、接点ポートフォリオが最適ということです。全ての投資家が接点ポートフォリオのみ保有するという仮定を置けば、接点ポートフォリオが市場平均になるというだけなので、あまり市場平均が最適ポートフォリオと言い過ぎるのもどうかとは思います。
なので、インデックス投資が優れているからと言って、現代ポートフォリオ理論の言う通りだ!と言うのは、違うのではと思ってます。現実世界では接点ポートフォリオと市場平均は乖離しているわけですからね。
はい、ということで、3回に渡って、現代ポートフォリオ理論について説明してみました。この知識が実際に役に立つかは別として、こういう理論を理解するというのは本当に楽しいものがありますね。
では!