タグ: 共分散

投稿日:

相関係数って何者？: 共分散のスケーリング



相関係数の性質を理解していても、その本質を理解している人は意外と少ないんじゃないでしょうか。
＊かくいう私も最近まで理解してませんでした。

相関係数の性質


相関係数は2種類のデータの関連性を示すものです。
-1~1の値を取り、下記のような性質を持つことが知られてます。

  • 相関係数が1に近い：同傾向が強い
  • 相関係数が-1に近い：反対傾向が強い
  • 相関係数が0に近い：（直線的な）関連がない

この辺りは知ってる人も多いと思います。

今回考えたいのは、よく知られた性質の話ではなく、一体どこからこのようなものが出てきたのかということです。

相関係数とは何者


まず相関係数の定義を見てみます。２種類のデータ列X, Yがあったとき、

$$ 相関係数= \frac{共分散}{Xの標準偏差\times Yの標準偏差}$$

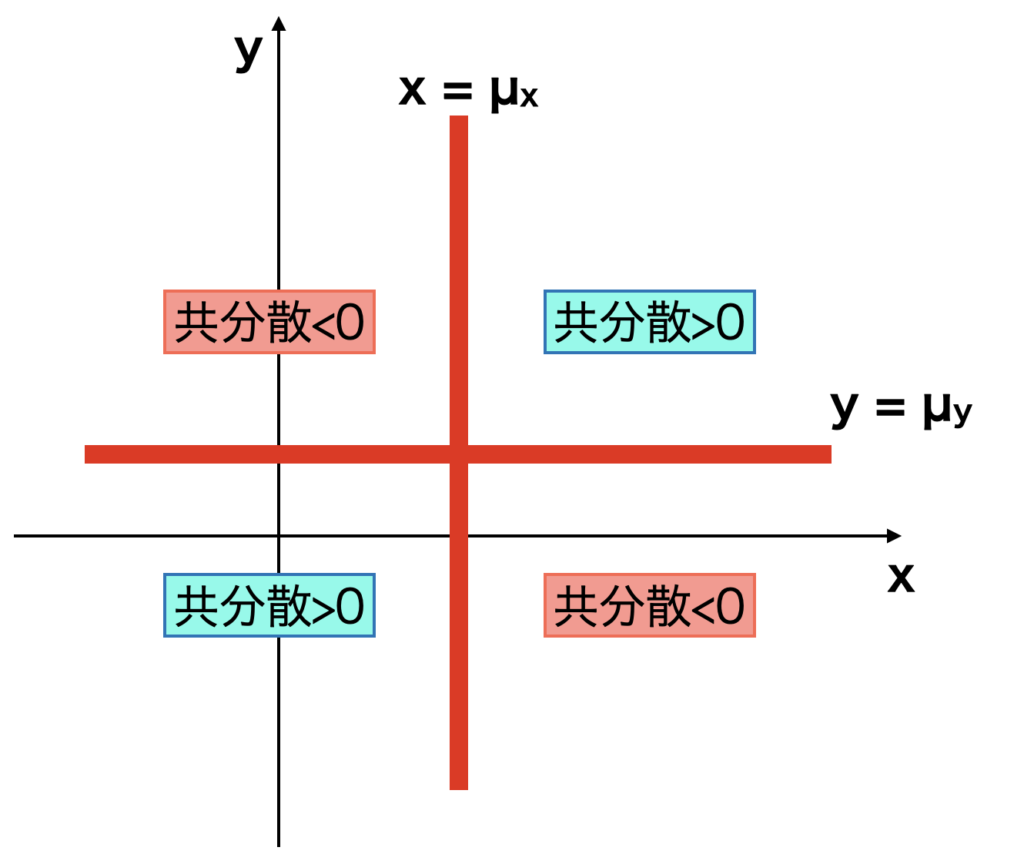
共分散をX, Yの標準偏差の積で割ったものですね。なぜこのような式になるのか。前回の記事で書いたように、共分散は二つのデータ列の傾向を示してます。

共分散の本質を定義から考える

しかし、共分散の値の大きさから傾向の程度を判断する基準がありません。例えば共分散が100だから同傾向の度合いが大きいとか、30だから小さいとか言えないわけです。なぜかというと、傾向の程度はX,Yの分散との比で決まる相対的なものだからです。

これは共分散の役割から考えると分かります。

合計(X+Y)の分散 = Xの分散+Yの分散+共分散

上式のように共分散はX、Yの傾向から合計の分散の値を調整するものです。
分散はXとYの単純な足しあわせにならず、共分散項による調整を受けるということです。

なので、例えば下記二つの例では同じ共分散100でも意味が異なるわけです。

  • Xの分散, Yの分散 = 110, 130のときの共分散100
  • Xの分散, Yの分散 = 1000, 800のときの共分散100

当然前者の方が合計の分散に与える影響が大きいため、前者の場合の方が同傾向の度合いは大きいと考えられます。

絶対的な判断基準を作る

「共分散の傾向の程度はX,Yの分散との比で決まる相対的なもの」です。

じゃあ、共分散をX, Yの分散で割ってあげれば絶対的な判断基準ができますよね。実際には分散ではなく、分散の平方根、つまり標準偏差で割ります。なので、下記の定義になるわけですね。

$$ 相関係数= \frac{共分散}{Xの標準偏差\times Yの標準偏差}$$

そして、この式の右辺は必ず-1 ~ 1となります。
この証明はググればいろいろ出てくるので割愛します。

まとめ

はい、ということで、共分散のままでは傾向の度合いに対する判断基準がないので、

標準偏差で割ることで絶対的な判断基準を作ったと、

そしてそれが相関係数と名付けられたということですね。

では。

投稿日:

共分散の本質を定義から考える

共分散ってややこしいですよね。

ネットで調べても定義が出てくるだけで、そもそもどこからこのような考え方が出てきたのかよくわからん、、、と私は思ってました。

一応高校でも習ってるみたいなんですけどね。

全く覚えてませんw

ただ、投資でもよく使用する相関係数は共分散を-1~1までの値にスケール変換したものですし、現代ポートフォリオ理論にも関係してくる話なので、共分散を理解することって実は大事なことなんじゃないかなーと思ってます。

共分散の前にまず分散について

分散(\( \sigma^2 \))は平均からのばらつき具合ですね。平均との差の二乗の平均で定義されます。

$$\sigma^2 = \frac{1}{n} \sum (x-\mu)^2 $$

例えば、企業Xの株価が下記だった場合、計算は割愛しますが、分散は125となります。

4月5月6月7月
株価1001109080

企業Yの株価が下記だった場合、分散は725となります。

4月5月6月7月
株価230200180250

共分散とは

今回考えたいのは二つのデータを足し合わせたときに、分散はどのようになるかです。

4月5月6月7月
株価X1001109080
株価Y230200180250
合計330310270330

つまり合計の分散ですね。計算すると分散は600になります。
ただ、ここで知りたいのは分散の値そのものではなく、合計の分散とX, Yそれぞれの分散の関係性です。
単純な足し合わせではなさそうです。

分散の定義から、

$$ \begin {eqnarray} \sigma_{X+Y} ^2 &=& \frac{1}{n} \sum (X+Y-\mu_{X+Y})^2 \\
&=& \frac{1}{n} \sum (X+Y-(\mu_{X}+\mu_{Y})^2) \\
&=&\frac{1}{n} \sum (X-\mu_{X})^2 + \frac{1}{n} \sum (Y-\mu_{Y})^2 + 2\times \frac{1}{n} \sum (X -\mu_{X})(Y – \mu_{Y})\\
&=&\sigma_{X}^2+\sigma_{Y}^2 + 2\times \color{red}{\frac{1}{n} \sum (X-\mu_{X})(Y-\mu_{Y})} \end{eqnarray}$$

この赤色の項こそ共分散の正体です。分散の定義式から導かれるものですね。
つまり、合計の分散 = Xの分散+ Yの分散 + 2\(\times \)共分散
となるわけです。

共分散項が何を意味しているか考えてみましょう。

共分散項の意味

平面を\( x=\mu_{X}, y=\mu_{Y} \)で４つのグループに分けると、右上と左下にデータが多い場合、つまりX, Yが同傾向の場合、共分散項は正になり、左上と右下にデータが多い場合、つまり反対の傾向の場合は負になります。また、X,Yがランダムに散らばっていた場合は共分散は0に近くなります。


つまり共分散の意味するところは二つのデータの傾向になります。

したがって二つのデータ群の傾向から\( \sigma_{X+Y} \) の値を調整する、これが共分散項の役割ですね。
データが同傾向であれば共分散>0になるので分散は大きくなり、データが反対傾向であれば共分散<0となり分散は小さくなります。
もし、無関係であれば共分散=0となり、分散はXとYの分散の単純な足しあわせになります。

今回挙げた株価の例では、共分散は-125となります。
確かにXとYの株価の値動きは反対方向ですよね。

よって、
合計（X+Y）の分散＝125+725 + 2 \(\times \) (-125) = 600

となり、最初に算出した分散と一致してますね。

なんだかスッキリした気分です。

相関係数については次回書きたいと思います。