以前、2銘柄ポートフォリオによってなぜリスクが下がるか説明しました。
1銘柄の場合、選択できるリスク・リターンの組み合わせは点となります(A社だけ、もしくはB社だけ)。2名柄の場合、選択できるリスク・リターンの組み合わせは線に拡大されます。A社、B社の組み入れ比率を変えることで、下記曲線状のリスク・リターンを自由に選択するすることができるようになります。
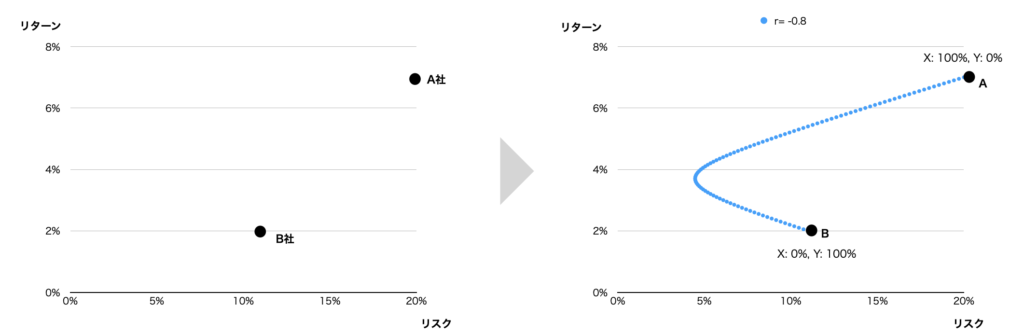
では、銘柄数をさらに増やしていくとどうなるのか。これが今日のテーマです。
3銘柄ポートフォリオ
銘柄を3つに増やしたときのリスク・リターンの関係はどうなるのか。組み入れ比率を変化させたときのシミュレーション結果は下記のようになります。(3銘柄ポートフォリオのリスクとリターンの式は書くのがめんどうなので割愛しますw平均と分散の定義から導けます。)
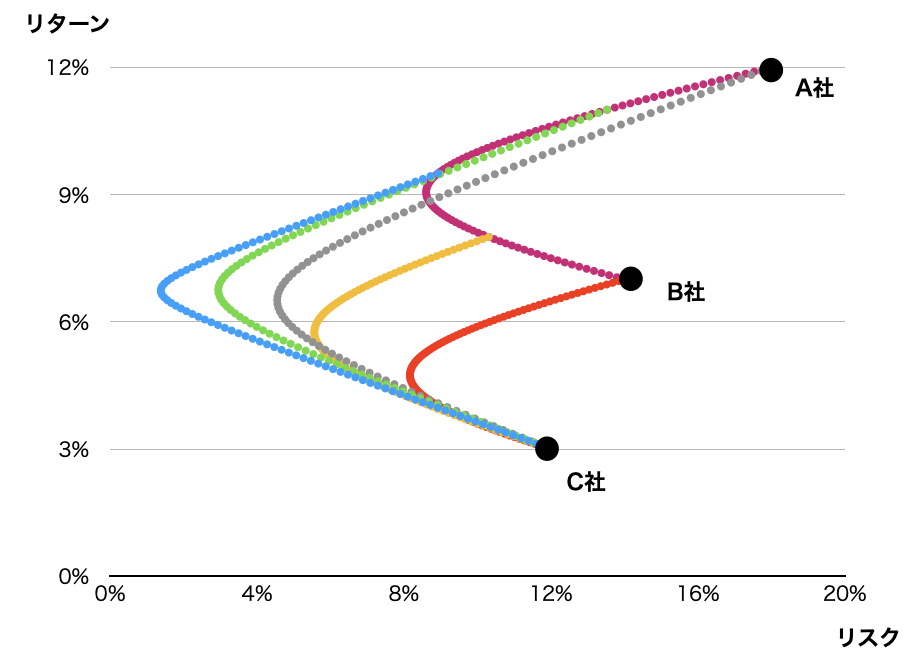
それぞれのリターン・リスク、相関係数は下記としました。
| リターン | リスク | |
| A社 | 12% | 18% |
| B社 | 7% | 14% |
| C社 | 3% | 12% |
| 相関係数 | |
| AとB | -0.4 |
| AとC | -0.8 |
| BとC | -0.2 |
3銘柄になると変数が多くなるので、例えばA:B = 50 : 50のポートフォリオを一つの銘柄と考えて、Cとこの銘柄の2銘柄ポートフォリオの曲線を描く、ということをしています。
それぞれの曲線がどの2銘柄の曲線かを示したのが下記です。6パターンの組み合わせで曲線を描いてます。
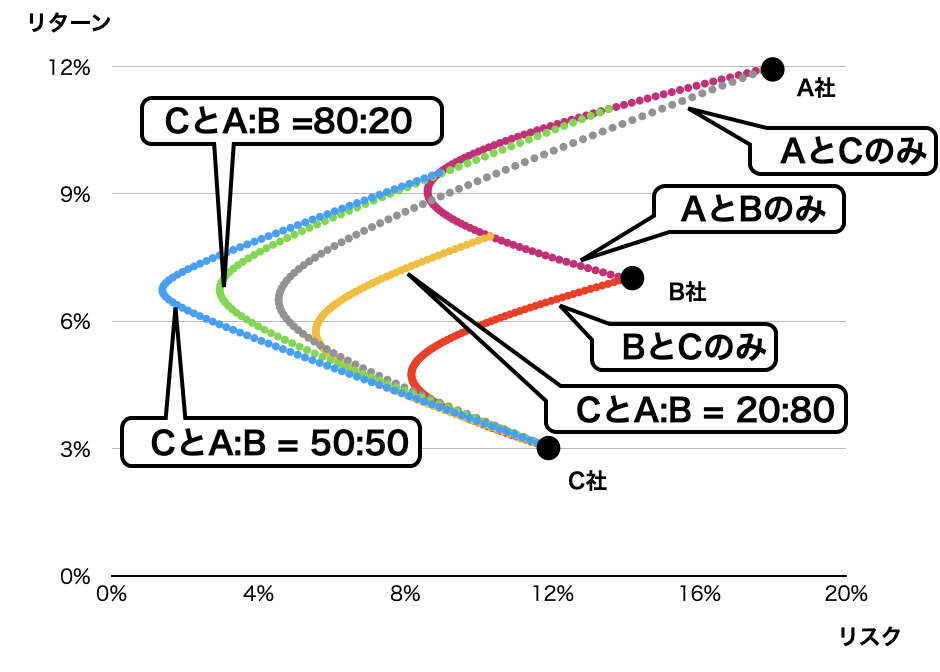
A:Bの比率をもっと細かく変えていけば、次第に内側が塗りつぶされた面になるでしょう。つまり、3銘柄ポートフォリオでは、面上の点からリスク・リターンを自由に選択できるようになります。

N銘柄ポートフォリオ
さらに銘柄数を増やしていくと、3銘柄のときよりも選択できる面の大きさが広がっていきます。そして、その中に全ての銘柄が含まれることになります。

したがって、ポートフォリオの銘柄数を増やしていけば、様々なリターン・リスクの組み合わせを実現することができるのです。
さて、このように銘柄数を増やせば選択肢を増やせるのですが、どの組み合わせが最も良いのでしょうか。
これはまた別の機会に。
