人間って普段何気なく「見る」という行為をしていますが、実はとても奥深い行動なんじゃないかと思うんです。
見ているものは同じでも、人によって見え方、感じ方が違うというのはよく聞く話ですが、このように「見る」という行為は何かフィルターをかけたり、非対称性を生んだりするような行為のような気がしています。
私がこのように感じたきっかけはというと、学生時代まで遡ります。
その頃の私は研究上、夜通し顕微鏡を覗くこともあるぐらい、顕微鏡と密接な関係にありました。なんとも悲惨な学生生活ですねw
理系学生にはあるあるかもしれません。
そうした生活の中で、私は光学顕微鏡についてとても不思議に感じていることがありました。若干専門知識も入るので、よく分からんという人はスルーしてください。
顕微鏡の光軸をz軸、光軸に垂直な平面をx-y平面と呼びます。分かりやすく言うと、画像となる面がx-y平面で、それに対して垂直な軸がz軸です。
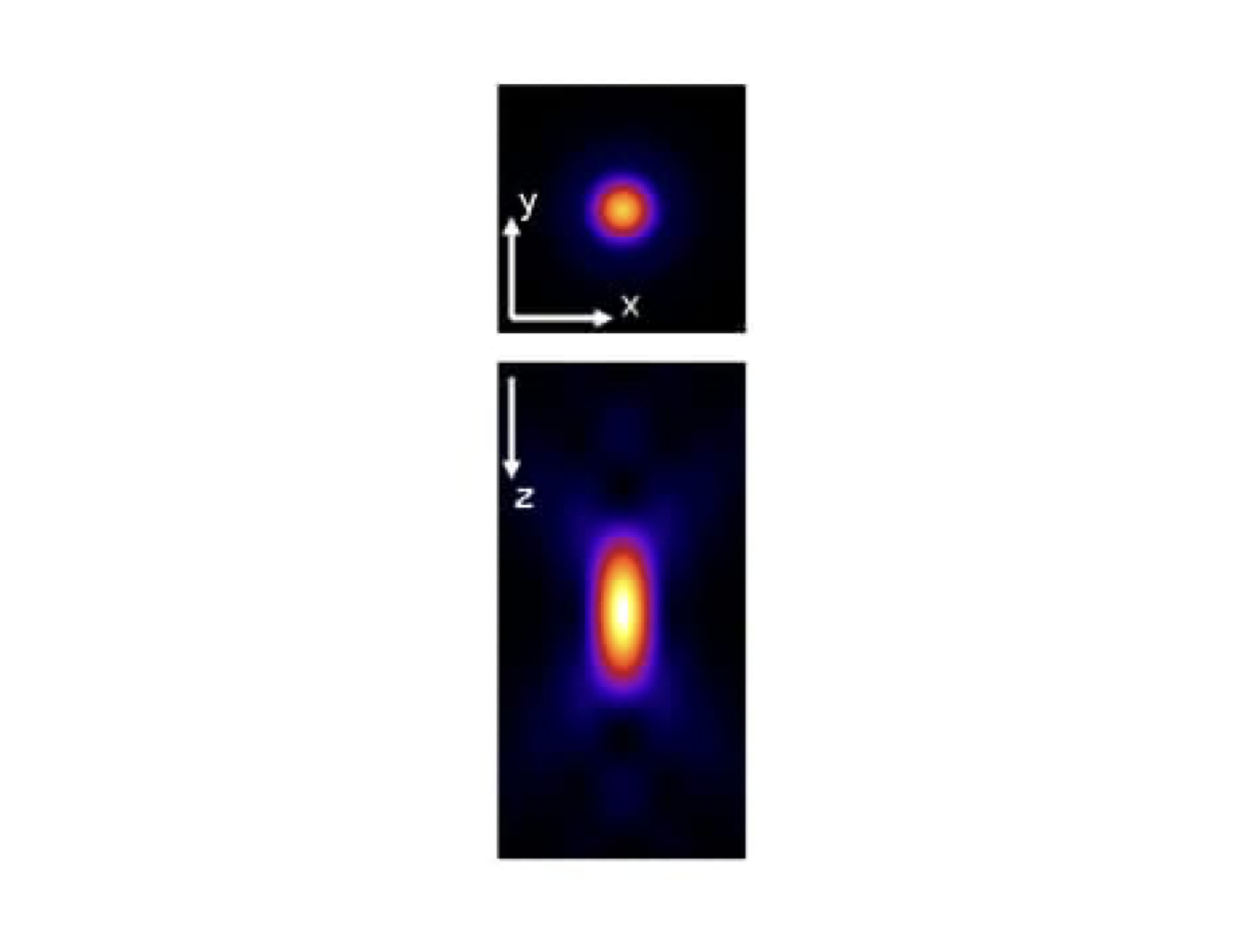
何が私にとって不思議だったかというと、x-y平面上の分解能とz軸方向の分解能が異なるという点です。どう異なるかというと、下図のような感じです。

なんだこれはという感じかもしれません(笑)詳細を書くと長くなってしまうので簡単に説明すると、点光源を顕微鏡を通して観察したときに、どのように見えるかを示しています。色は光の強度を表していて、点を観察したとき、このように広がりを持った像になります。つまり、点を観察しても点にはならず、ぼやっと広がった像になるということです。そしてこの広がり具合を分解能と定義してます。上の図がx-y平面、下の図がz軸方向の広がりを表しています。
この図を見て分かるように、x-y平面とz軸方向では広がり方が違います。x-y平面は円状に広がっているのに対して、z軸方向は楕円状になっています。これが何を意味するかというと、顕微鏡で点を観察すると、3次元空間ではz軸方向に伸びた楕円体として観測されるということです。点を点として見ることはできず、楕円体になってしまうんですね。
私にとってこれはとても興味深いことでした。x-y平面とz軸方向で非対称性が生まれているわけですが、これは顕微鏡で「見る」という行為によって生じたものです。物はそこにあるだけなのに、ありのままで観察することはできない。見るという行為そのものによって、非対称性が生じてしまうのです。
おもしろいな〜と思っていたんですが、あるときふと思いました。
「物はそこにあるだけなのに、ありのままで観察することはできない。」
これって、物だけじゃなくて日々の出来事にも当てはまるんじゃないかと。人は辛い経験、悲しい経験、楽しい経験などいろんな経験をすると思いますが、事実としてはその出来事があったというだけです。そこに楽しい、辛い、悲しい、などの意味付けしているのは人間自身です。つまり、実際はその出来事が起こったという事実があるだけなんですが、事実をありのままに捉えるのは難しくて、人それぞれ意味付けをして受け取っているということですね。
その意味づけはその人の性格や、経験から決まる物なので、様々です。だから、同じものを見ていても人によって感じ方が異なるんですね。人間自身が事実を変換するフィルターのようなものなのかなと思ってます。
「見る」っておもしろくないですか?
では!