
共分散ってややこしいですよね。
ネットで調べても定義が出てくるだけで、そもそもどこからこのような考え方が出てきたのかよくわからん、、、と私は思ってました。
一応高校でも習ってるみたいなんですけどね。
全く覚えてませんw
ただ、投資でもよく使用する相関係数は共分散を-1~1までの値にスケール変換したものですし、現代ポートフォリオ理論にも関係してくる話なので、共分散を理解することって実は大事なことなんじゃないかなーと思ってます。
共分散の前にまず分散について
分散(\( \sigma^2 \))は平均からのばらつき具合ですね。平均との差の二乗の平均で定義されます。
$$\sigma^2 = \frac{1}{n} \sum (x-\mu)^2 $$
例えば、企業Xの株価が下記だった場合、計算は割愛しますが、分散は125となります。
| 4月 | 5月 | 6月 | 7月 | |
| 株価 | 100 | 110 | 90 | 80 |
企業Yの株価が下記だった場合、分散は725となります。
| 4月 | 5月 | 6月 | 7月 | |
| 株価 | 230 | 200 | 180 | 250 |
共分散とは
今回考えたいのは二つのデータを足し合わせたときに、分散はどのようになるかです。
| 4月 | 5月 | 6月 | 7月 | |
| 株価X | 100 | 110 | 90 | 80 |
| 株価Y | 230 | 200 | 180 | 250 |
| 合計 | 330 | 310 | 270 | 330 |
つまり合計の分散ですね。計算すると分散は600になります。
ただ、ここで知りたいのは分散の値そのものではなく、合計の分散とX, Yそれぞれの分散の関係性です。
単純な足し合わせではなさそうです。
分散の定義から、
$$ \begin {eqnarray} \sigma_{X+Y} ^2 &=& \frac{1}{n} \sum (X+Y-\mu_{X+Y})^2 \\
&=& \frac{1}{n} \sum (X+Y-(\mu_{X}+\mu_{Y})^2) \\
&=&\frac{1}{n} \sum (X-\mu_{X})^2 + \frac{1}{n} \sum (Y-\mu_{Y})^2 + 2\times \frac{1}{n} \sum (X -\mu_{X})(Y – \mu_{Y})\\
&=&\sigma_{X}^2+\sigma_{Y}^2 + 2\times \color{red}{\frac{1}{n} \sum (X-\mu_{X})(Y-\mu_{Y})} \end{eqnarray}$$
この赤色の項こそ共分散の正体です。分散の定義式から導かれるものですね。
つまり、合計の分散 = Xの分散+ Yの分散 + 2\(\times \)共分散
となるわけです。
共分散項が何を意味しているか考えてみましょう。
共分散項の意味
平面を\( x=\mu_{X}, y=\mu_{Y} \)で4つのグループに分けると、右上と左下にデータが多い場合、つまりX, Yが同傾向の場合、共分散項は正になり、左上と右下にデータが多い場合、つまり反対の傾向の場合は負になります。また、X,Yがランダムに散らばっていた場合は共分散は0に近くなります。
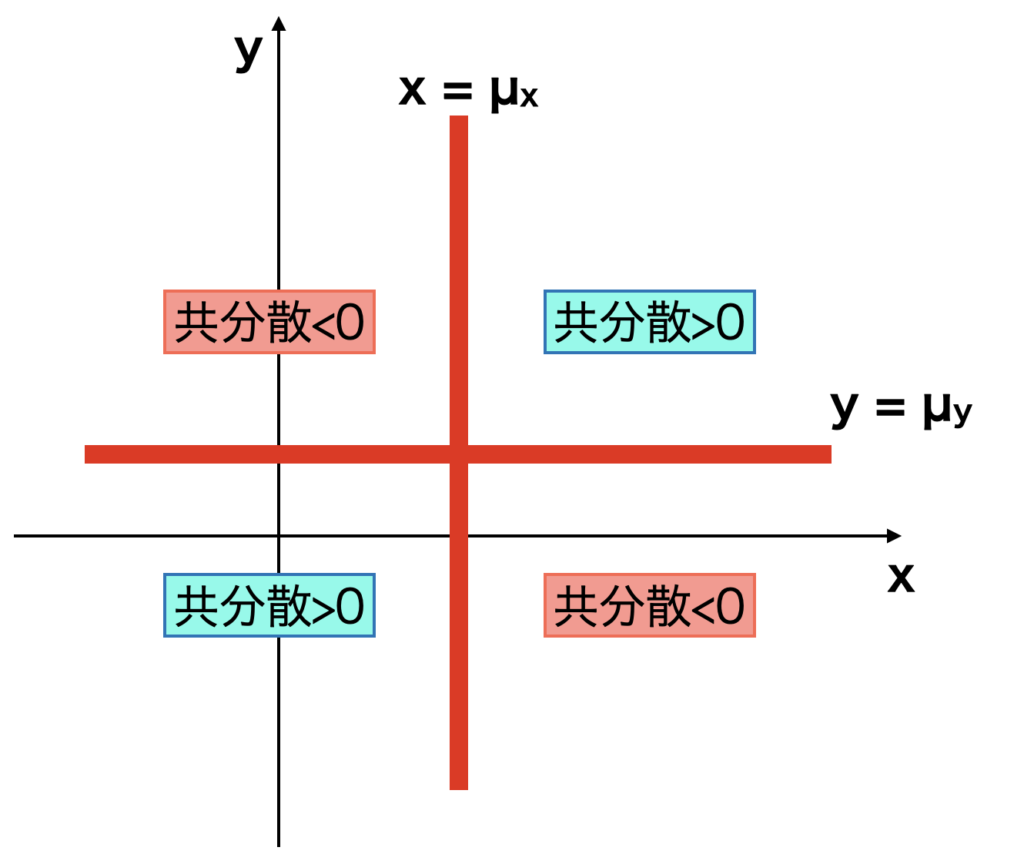
つまり共分散の意味するところは二つのデータの傾向になります。
したがって二つのデータ群の傾向から\( \sigma_{X+Y} \) の値を調整する、これが共分散項の役割ですね。
データが同傾向であれば共分散>0になるので分散は大きくなり、データが反対傾向であれば共分散<0となり分散は小さくなります。
もし、無関係であれば共分散=0となり、分散はXとYの分散の単純な足しあわせになります。
今回挙げた株価の例では、共分散は-125となります。
確かにXとYの株価の値動きは反対方向ですよね。
よって、
合計(X+Y)の分散=125+725 + 2 \(\times \) (-125) = 600
となり、最初に算出した分散と一致してますね。
なんだかスッキリした気分です。
相関係数については次回書きたいと思います。
