私はリスクが嫌いです。
横断歩道を渡るときに、信号無視して突っ込んでくる車がいないか何度も確認するほどビビりです。あと、道を歩いているときに背後に人がいるのも嫌ですね。このご時世いきなり刺される可能性もなきにしもあらずなわけですし。
一般的にもリスクは小さい方が好まれるでしょう。ただし、株式において個別の銘柄のリスクとリターンはトレードオフの関係で、ハイリスク・ハイリターン、ローリスク・ローリターンなのです。なので、リスクを小さくしようとすれば、リターンも小さくなってしまう。
悩ましい問題ですね。
これを解決してくれるのがポートフォリオ効果です。ポートフォリオとは複数の銘柄を保有するだけのことですが、これにによって、下記のようなリターン、リスクの組み合わせが実現できるようになります。
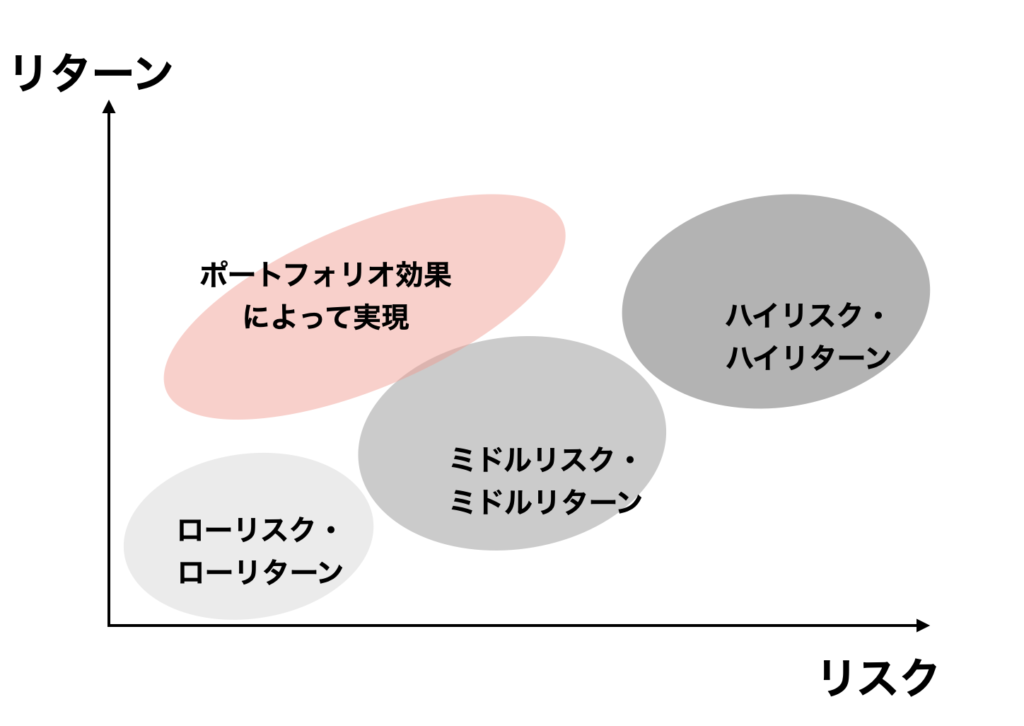
ポートフォリオ効果の理論的説明
なぜこのようなことが可能か、ガチガチの理論面から説明したいと思います。
X株とY株の二つの株式からなるポートフォリオを考えます。
X株の保有割をaとし、このポートフォリオをZとすると、
$$Z = aX + (1-a)Y $$
ポートフォリオの平均\(\mu_{Z} \)と分散\(\sigma_{Z}^2 \)は、相関係数をrとして
$$ \begin{eqnarray}
\mu_{Z} &=& a\mu_{X} + (1-a)\mu_{Y} \\ \\
\sigma_{Z}^2 &=& \frac{1}{n} \sum (Z-\mu_{Z})^2 \\
&=& \frac{1}{n} \sum (aX+(1-a)Y – (a\mu_{X}+(1-a)\mu_{Y}))^2 \\
&=& …\\
&=& a^2\sigma_{X}^2 + (1-a)^2\sigma_{Y}^2 + 2a(1-a)r\sigma_{X} \sigma_{Y}\\
\end{eqnarray}$$
途中かなり端折ってしまいましたが(数式入力けっこうしんどい、、、)、このように平均と分散はaの媒介変数表示で表すことができます。
ここで平均(\(\mu_{Z} \))はリターン、分散の平方根、つまり標準偏差(\(\sigma_{Z} \))はリスクを意味してます。
なので、この2式からリターン・リスクの関係が分かるということですね。
リターンはX,Yの単純な加重平均ですが、リスクは何やら複雑な式になってます。。
増減表を書けばリターン-リスクのグラフの全体像が分かりますが、めんどくさいのでそこまでは書きません。一応自分ではやってみました(暇人w)
数式のシミュレーション
増減表は書きませんが、エクセルでシミュレーションを行なってみたので、その結果を載せたいと思います。条件として、下記のように設定し、Xの保有割合aと相関係数rを変えたときのリターン・リスクの関係を見てみます。
- X株:リターン 7%, リスク 20%
- Y株:リターン 2%, リスク 11%
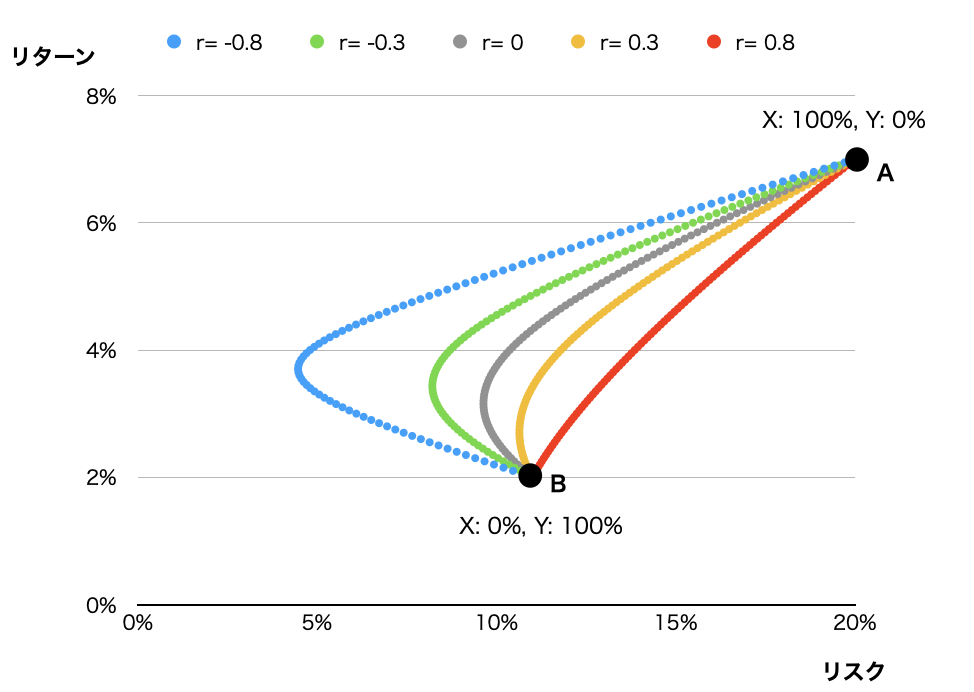
点AはX株のみ保有している状態(つまりa: 100%)、そこからaを変化させて点B(Y株のみ保有)に至るまでの軌跡を示してます。色は相関係数rの違いを表してます。
これらの軌跡は左側に膨らんでいる、つまりリスクが低減されていることが分かります。
このときポイントは三つあって、
- リターンはX,Yの加重平均である
- リスクはX,Yの加重平均よりも小さくなる
- リスク低減は相関係数が小さいほど効果が強い
1,2はリスクのみが低減されることを意味していて、「ローリスク・ローリターン」の原則を覆したことになります。たしかに点Bから出発すると、リスクは下がっているにもかかわらずリターンは上がっていることが分かります!図1に示した部分を実現できていますね。
3については、逆の値動きをする2銘柄を組み合わせた方がリスク低減効果が大きいことを示してます。たしかに相関係数-0.8の場合が最も左に膨れています。逆に、相関係数が0.8の場合を見れば分かる通り、1に近いほど効果は薄れます。まあ直感的にもそうですよね。逆の値動きをするもの同士は相殺してリスクは小さくなる。それが理論的にも示されたということです。
まとめ
ということで、ポートフォリオ効果によってなぜリスクが低減するのか理論的に説明してみました。
ここで気になるのが、リスク・リターン曲線上のどの点を買うのがいいのか?ということです。
たしかに、X, Yを組み合わせればリスクを低減できますが、リターンが最も高いのはXのみ保有した場合です。ハイリスク・ハイリターンを好む人はXのみを保有するでしょう。
最適なポートフォリオは何か?これはとても興味深い問題です。
また別のときに書きたいと思います。
では。
